Podcast: Play in new window | Download (Duration: 6:14 — 8.6MB)
Abbonniere den Podcast Apple Podcasts | Spotify | Amazon Music | RSS
Eine Reise in die unendlichen Weiten der Zahlenwelt
Was ist Unendlichkeit und wie funktioniert sie in der Mathematik? Begleite uns auf eine Reise durch unendliche Zahlenreihen, Paradoxe und die seltsame Welt der Mathematik!
Unendlichkeit klingt mysteriös, fast wie ein magisches Konzept – aber es ist ein zentraler Begriff in der Mathematik! Man könnte meinen, Unendlichkeit bedeutet einfach, dass etwas „nie endet“. Aber wie sieht das in der Mathematik wirklich aus? Unendlichkeit beschreibt Dinge, die kein Ende haben – wie Zahlenreihen oder das Universum. Es geht aber nicht nur um riesige Zahlen, sondern auch um die kleinen Dinge, wie unendlich viele Zahlen zwischen 0 und 1!
Unendlichkeit in der Mathematik: Mehr als nur große Zahlen
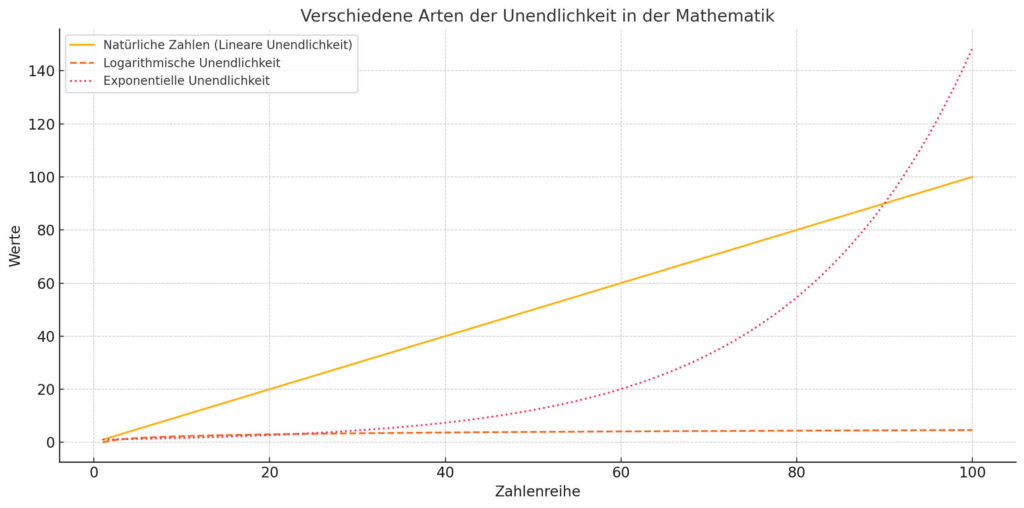
Unendlichkeit bedeutet in der Mathematik nicht nur, dass eine Zahlenreihe endlos weitergeht – es gibt verschiedene Arten von Unendlichkeiten! Ein Beispiel dafür ist die Reihe der natürlichen Zahlen: 1, 2, 3, 4 … Diese Reihe hört nie auf. Aber auch in den Dezimalzahlen steckt Unendlichkeit, wie bei 0,333… oder der Zahl Pi, die unendlich viele Stellen nach dem Komma hat. Sogar zwischen zwei Zahlen, wie 0 und 1, gibt es unendlich viele Zahlen. Verrückt, oder?
Symbole der Unendlichkeit

Das Symbol der Unendlichkeit (∞) hast du bestimmt schon mal gesehen – es sieht aus wie eine liegende 8. Dieses Symbol wurde erstmals im 17. Jahrhundert vom Mathematiker John Wallis verwendet. Aber warum gerade dieses Symbol? Es soll die Idee der Endlosigkeit darstellen, etwas, das nie aufhört oder einen Anfang oder ein Ende hat. In der Mathematik nutzen wir es, um unendliche Mengen oder Vorgänge zu beschreiben, die niemals enden.
Unendliche Mengen: Was bedeutet das?
In der Mathematik gibt es viele Beispiele für unendliche Mengen. Die einfachste unendliche Menge ist die Menge der natürlichen Zahlen: 1, 2, 3, 4 und so weiter – sie hören nie auf. Aber wusstest du, dass es unterschiedliche Arten von Unendlichkeiten gibt? Zum Beispiel gibt es auch zwischen zwei natürlichen Zahlen (wie 1 und 2) unendlich viele Brüche. Spannend wird es, wenn man entdeckt, dass einige Unendlichkeiten größer sind als andere!
Paradoxe der Unendlichkeit
Das Paradoxon von Hilberts Hotel zeigt, wie absurd Unendlichkeit manchmal wirken kann. Stell dir ein Hotel mit unendlich vielen Zimmern vor, das komplett ausgebucht ist. Wenn ein neuer Gast kommt, kann der Hotelmanager einfach alle Gäste um ein Zimmer verschieben – der Gast im Zimmer 1 geht in Zimmer 2, der in Zimmer 2 in Zimmer 3 usw. So wird plötzlich das Zimmer 1 frei, obwohl das Hotel „voll“ war. Dies illustriert, wie wir mit unendlichen Mengen anders umgehen müssen als mit endlichen Mengen. Das zeigt, dass Unendlichkeit mathematisch faszinierend, aber manchmal auch schwer zu begreifen ist.
Ein anderes, etwas weniger bekanntes Paradox ist das Banach-Tarski-Paradoxon: Es besagt, dass man einen Ball in endlich viele Stücke zerlegen und diese wieder zusammensetzen kann, um zwei Bälle der gleichen Größe zu erhalten – unter der Annahme, dass man mathematisch perfekte Schnitte machen kann. Das klingt verrückt und ist in der realen Welt natürlich unmöglich, aber zeigt, welche seltsamen Eigenschaften unendliche Mengen in der Mathematik haben können.
Unendlichkeit in der realen Welt
In der Physik und Astronomie sind Konzepte der Unendlichkeit besonders spannend. Das Universum dehnt sich ständig aus, aber ist es wirklich unendlich? Viele Wissenschaftler glauben, dass das Universum entweder unendlich groß ist oder zumindest keine klaren Grenzen hat. Das wirft spannende Fragen auf: Wenn das Universum unendlich ist, gibt es dann unendlich viele Sterne und Planeten? Und wenn es eine Grenze gibt, was kommt danach?
Ein weiteres Beispiel für Unendlichkeit in der realen Welt ist die Zeit. Laut aktuellen physikalischen Modellen hat die Zeit mit dem Urknall begonnen, aber es ist unklar, ob die Zeit jemals enden wird. Wenn sie unendlich weitergeht, was bedeutet das für das Universum und für uns?
Fazit: Warum Unendlichkeit wichtig ist
Unendlichkeit ist mehr als nur eine Idee – sie spielt eine entscheidende Rolle in Mathematik und Wissenschaft. Ohne das Konzept der Unendlichkeit könnten wir viele mathematische Probleme nicht lösen und keine Phänomene wie die Ausdehnung des Universums verstehen. Von der unendlichen Zahlenmenge bis zu den Paradoxa regt Unendlichkeit unser Denken an und zeigt, dass manche Dinge in der Welt keine Grenzen haben. Sie ist eine Brücke zwischen Mathematik und der Vorstellungskraft!
Hallo, ich bin der Betreiber des Blog und interessiere mich für allerlei Dinge. Wenn ich etwas neues gelernt habe, schreibe ich es hier in diesem Blog auf, um mein Wissen zu festigen. Gemeinsam mit den K.I.s GPT-4 und Midjourney erstelle ich diese Blogposts. Meine Aufgabe ist es, Quellen für die Aussagen zu finden, zu prüfen, den Sprachstil zu verbessern, sinnvolle Querverbindungen zu vergangenen Blogposts herzustellen und neue Blogpostthemen zu erstellen. Der Blog soll zeigen, wie eine sinnvolle Kollaboration zwischen Mensch und K.I. funktioniert und jungen Menschen komplexe Themen einfach erklären.





